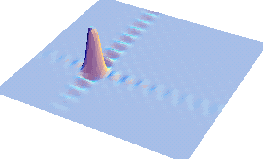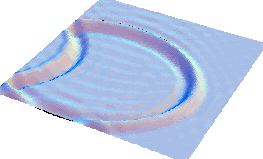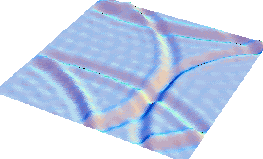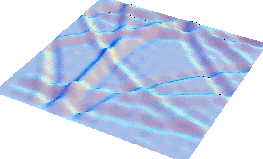
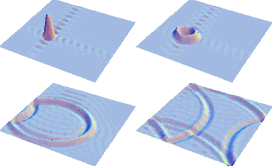
 |
Рассмотрим колебания прямоугольной мембраны. Пусть в начальный момент времени фома мембраны такова, как показано на рисунке вверху слева
(в данном случае это  ).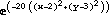
Мы увидим, что такой точечный импульс будет распространяться в виде кольцевой
волны (рис. вверху справа). Дойдя до краёв, эта волна будет отражаться и изменять знак
(рис, внизу слева), и после отражения - интерферировать (рис. внизу справа).
Мелкие колебания украшают картинку, однако они являются погрешностями математической
модели процесса, возникшей из-за конечности числа гармоник (25), по которым
раскладывали исходную функцию (на рисунке показан её вид после восстановления
по гармоникам).
В иллюстративных целях масштаб графиков по вертикали сильно увеличен.
|
