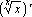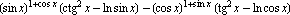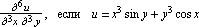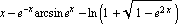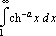| Занятие 2 |
| Операции математического анализа |
| Просмотрите справочную информацию по командам
Limit, D, Integrate, NIntegrate (справочные
статьи по этим командам, а так же и под другим командам, связанным с операциями
математического анализа, находятся в разделе Help/ Built-in-Functions/
Algebraic Manipulation/ Calculus |
Упражнение 9: Выполните следующие задания:
| a) |  | Ответ: ln x. |
| b) |  | Ответ: a/2 |
| c) | 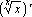 | Ответ:  |
| d) |  | Ответ:  |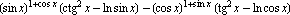
| e) | 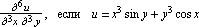 | Ответ: 6(sin x - cos x) |
| f) |  | Ответ:  |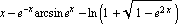
| g) | 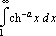 | Ответ:  |
| h) |  | Ответ: 2.05045 |
|
|
| Представление вещественных чисел |
Вещественное число в Mathematica характеризуется
двумя параметрами:
| Precision | - | общее количество знаков в числе |
| Accuracy | - | количество цифр после десятичной точки | |
В качестве примера выполните следующую ячейку:
|
a = 9876543210.01234567890123456789
Precision[a]
Accuracy[a]
|
 |
| 30 |
| 20 |
|
| Однако следует учитывать, что Precision[a] и
Accuracy[a] показывают количество знаков во внутреннем представлении числа,
тогда как на экране это число может отображаться с меньшим числом знаков: |
a = Sqrt[2]
Precision[a]
|
| 1.41421 |
| 16 |
|
| Здесь Mathematica выводит на экран лишь 6 знаков числа
a,тогда как в памяти машини она хранит значительно больше - 16 знаков. Их
можно вывести на экран, используя команду InputForm. |
| InputForm[a] |
| 1.4142135730951 |
|
Mathematica различает два типа внутреннего представления
вещественных чисел - числе с машинной точностью (mashine-precision numbers) и
числа с произвольной точностью (abitrary-precision numbers). Числа с машинной
точностью содержат фиксированное количество знаков, в типичном
случае - 16, так что значение Precision для них всегда равно 16. В отличие от них,
числа с произвольной точностью могут содержать произвольное,
практически сколь угодно большое число знаков, и значение Precision
для них может быть любым. Операции над числами с машинной точностью выполняются
быстрее, чем для чисел с произвольной точностью, однако использование чисел с
произвольной точностью позволяет получить практически сколь угодно точный результат.
При вводе вещественного числа Mathematica сама определяет, какой тип
представления ей следует использовать: если для числа вводятся только 16
знаков или меньше, то Mathematica представляет его как число с
машинной точностью (т.е. 16-значное), если же более 16 - то как число с произвольной
точностью, равной числу введённых знаков: |
Precision[210.]
Precision[9876543210.]
Precision[9876543210.0123456789] |
| 16 |
| 16 |
| 20 |
|
| Здесь в первых двух случаях Mathematica использовала
представление с машинной точностью, а в последнем - с произвольной точность.
Для того, чтобы определить, как именно представлено число, можно также
использовать тест MashineNumberQ |
MashineNumberQ[9876543210.]
MashineNumberQ[9876543210.0123456789] |
| True |
| False |
|
| т. е. тест подтверждает, что первое вещественное
число Mathematica представляет как число с машинной точностью, а
второе - иначе, т. е. как число с произвольной точностью. |
| Точность численных вычислений |
| Следует различать точность представления вещественного
числа от точность самого этого числа как результата матопераций.
Скажем, интеграл, вычисленный с помощью NIntegrate: |
| a = NIntegrate[11 Cos[11 x], {x, 0, π/2}]; |
|
| по умолчанию представляется как число с машинной точностью, т.е. содержащее 16 знаков: |
MashineNumberQ[a]
Precision[a]
InputForm[a] |
| True |
| 16 |
| -1.0000000000000029 |
|
Однако можно видеть, что не все из этих 16 знаков
является верными - точное значение интеграла равно -1, так что последние два
знака - неверные. Таким образом, в общем случае точность результата численных
вычислений отличается от точности его представления.
Алгоритмы, используемые Mathematica для численных
вычислений, позволяют оценить точность получаемого результата, и вычисления
прекращаются, как только требуемая точность достигается. Если же достичь её
Mathematica не может, то она выдаёт коммментарий, в котором она высказывает
свои соображения относительно причин этого и способов улучшения результата.
При этом следует учитывать, что Mathematica, разумеется, не может определить
действительную точность результата, она может только оценть её, и её оценка
может отличаться от действительной точности.
Требуемая точность задаётся с помощью
опций PrecisionGoal и AccuracyGoal:
| PrecisionGoal | - | общее число требуемых точных
знаков в результате (по умолчанию 6 знаков); | | AccuracyGoal |
- | число требуемых точных знаков после десятичной точки в результате
(по умолчанию не определено) |
Следующие примеры поясняют использование
этих опций: |
| NIntegrate[Cos[Cos[x]], {x, 0, π}] |
| 2.40394 |
|
| Здесь было достигнуто требуемое количество точных знаков
в результате, т. е. 6, и эти 6 знаков выведены на экран. |
NIntegrate[Cos[Cos[x]], {x, 0, π}, PrecisionGoal  10] |
| 2.40394 |
|
| Здесь было установлено более высокое значение требуемой точности -
10 знаков, и при вычислениях эта точность была успешно достигнута (по оценке Mathematica.
Однако на экран было выведено только 6 знаков результата. Это связано с тем, что
Mathematica смогла обойтись только числами с машинной точностью, а для
таких чисел по умолчанию выводится только 6 знаков. Чтобы вывести все полученные знаки,
можно использовать команду InputForm |
a = NIntegrate[Cos[Cos[x]], {x, 0, π}, PrecisionGoal 10];
InputForm[a] |
| 2.403939430634413 |
|
| Здесь были выведены все 16 знаков, содержащизся в числе a.
Однако, в соответствии с установкой PrecisionGoal 10, лишь первые
10 знаков можно считать верными (по оценке Mathematica). Некоторая часть
остальных знаков тоже может быть верной, но этого утверждать нельзя. |
| a = NIntegrate[Cos[Cos[x]], {x, 0, π}, PrecisionGoal 18] |
- NIntegrate::ploss :
Numerical integration stopping
due to loss of precision. Achieved neither the requested PrecisionGoal nor AccuracyGood;
suspect one of the following^ highly oscillatory integrand or the true value of the integral is 0. If
your integral is oscillatory try using the option Method Oscillatory in NIntegrate. |
| 2.40394 |
|
| Здесь Mathematica не смогла достичь требуемой точности.
Но её всё-таки можно достигнуть, если использовать другие опции команды NIntegrate. В данном
случае следует увеличить значение опции WorkingPrecision. Эта опция определяет точность
представления чисел, используемых во внутренних вычислениях в процессе интегрирования.
По умолчанию её значение равно 16, и, разумеется, используя такие числа, нельзя получить
результат с точностью, болье 16. Если же мы повысим WorkingPrecision, то требуемая точность
может быть достигнута: |
| NIntegrate[Cos[Cos[x]], {x, 0, π}, PrecisionGoal 18, WorkingPrecision 20] |
| 2.403939430634412998 |
|
Однако в этом случае Mathematica вынуждена использовать
во внутренних вычислениях числа с произвольной точностью, поэтому время вычислений
существенно возрастает.
Если увеличение WorkinkPrecision не помогает, или время
вычислений чрезмерно возрастает, то надо использовать другие опции. Их смысл можно
определить с помощью справочной системы, а значения, установленные по умолчанию -
с помощью команды Options: |
| Options[NIntegrate] |
| {AccuracyGoal ∞, Compiled True,
GaussPoints Authomatic, MaxPoints Authomatic; MaxRecursion 6,
Method Authomatic, MinRecursion 0, PrecisionGoal Authomatic;
SingularityDepth 4; WorkingPrecision 16} |
|
Упражнение 10:
| a) | Вычислите с точностью 25 знаков интеграл |  | (используйте опции PrecisionGoal и WorkingPrecision). |
| b) | Вычислите с точностью 10 знаков интеграл |  | (используйте опции PrecisionGoal и MinRecursion). |
Ответы: a) 2.050446234534731259656830 b) 4.727991543
|
|