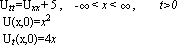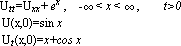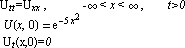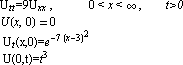| Set (=) | - | непосредственное присвоение; |
| SetDelayed (:=) | - | отложенное присвоение. |
До тех пор, пока эти операции используются лишь для присвоения переменным каких-либо определённых значений, разницы между ними практически нет - совершенно всё равно, выполнить присвоение a=10 или a:=10 - результат получится одним и тем же - a приобретёт значение 10. Но если одной переменной присваивается значение другой, то разница становится принципиальной. Для того, чтобы пояснить эту разницу, рассмотрим следующий простой пример.
Введём переменную x и присвоим ей значение 1:
| x = 1 |
| 1 |
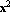 , но для f используем непосредственное
присвоение:
, но для f используем непосредственное
присвоение:f=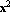 |
| 1 |
g:=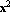 |
| f g |
| 1 |
| 1 |
| x = 2; f g |
| 1 |
| 4 |
Таким образом, различие между непосредственным и отложенным присвоениями состоит в следующем: при непосредственном присвоении значение вычисляется в момент присвоения и записывается в переменную, а при отложеном - новая переменная привязывается к старой, и её значение вычисляется при использовании
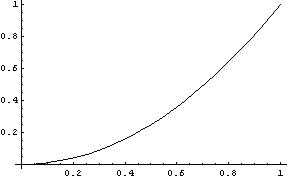
Особенно наглядным это различие становится, если построить графики f и g в зависимости о x:
| Plot[f, {x, 0, 1}] |
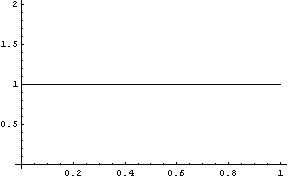 |
| - Graphics - |
| Plot[g, {x, 0, 1}] |
 |
| - Graphics - |
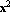 вычисляется заново, в соответствии с текущим значением x.
вычисляется заново, в соответствии с текущим значением x.Для того, чтобы отменить присвоения, выполненные для какой-либо переменной, следует выполнить для неё операцию Clear. Так, после выполнения команды
| Clear[x, f, g] |
| x f g |
| x |
| f |
| g |
| непосредственной | Rule | ( ) ) |
| отложенной: | RuleDelayed | (:>) |
Чтобы выполнить некоторую подстановку x
 y во
всех частях какого-либо выражения expr, следует применить к нему функцию ReplaceAll:
y во
всех частях какого-либо выражения expr, следует применить к нему функцию ReplaceAll:RepalceAll[expr, x
 y] или expr /. x
y] или expr /. x y
yНапример:
x + y /. x  1 1 |
| 2 x |
x + y /. {x  1, y 1, y  2} 2} |
| 3 |
x + y /. {{x  1, y 1, y  2}, {x 2}, {x  10, y 10, y  20}} 20}}n! /. {{n  1}, {n 1}, {n  2}, {n 2}, {n  3}} 3}} |
| {3, 30} |
| {1, 2, 6} |
 ; ;rulelist:=Solve[p == 0, x] |
| f = p /. rulelist Simplify[f] |
| rootlist = x /. rulelist |
| root1 = rootlist[[1]] root2 = rootlist[[2]] |
| Clear[x,f,p,rulelist,rootlist,root1,root2] |
| Упражнение 10: Ознакомбтесь с командой численного решения полиномиальных уравнений NSolve. Найдите с её помощью все корни уравнения 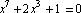 Используя операции с подстановками и списками, как показано выше, выполните следующие операции: a) Оцение точность решения путём постановки в исходное уравнение; b) Введите переменные root1, root2, ... и присвойте им значения корней. |
Один из способов задания функции пользователем можно в облем виде представить следующим образом:
Name[parameter1_, parameter2_, ...]=expression,
или
Name[parameter1_, parameter2_, ...]:=expression,
т.е. после имени функции в квадратных скобках через запятую перечисляются её формальные параметры, т.е. аргументы, от которых она зависит, причём после каждого параметра ставится знак подчёркивания "_"; затем идёт знак непосредственногоъ или отложенного присвоения ("=" или ":="), и выражение, соответствующее данной функции; это выражение должно зависеть от указанных формальных параметров, причём эти параметры пишутся уже после знака подчёркивания.
Например:
f[x_]=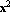 |
| f[-1/3] f[0.1] f[a] f[a+b] |
 g[3, 4] g[a + b, 2] |
 | ||||||
| Norm2[Sin, 0, π] Norm2[f, 0, 1] | ||||||
Упражнение 11: Введите в Mathematica формулу
Даламбера для общей задачи о колебаниях бесконечной струны: Постройте с её помощью решение для следующих частных задач:
Представьте решения графически на интервале -10 < x < 10 для t = 0.1; 1; 10, а также в виде трёхмерного графика на области -2 < x < 2, 0 < t < 2. |
| y[x_]:=x/; x≥0 y[x_]:=0/; x<0 | ||
| y[2] | ||
| y[-2] | ||
Plot[y[x], {x, -1, 1}, PlotStyle  RGBColor[1, 0, 0]] RGBColor[1, 0, 0]] | ||
Упражнение 12: Постройте в Mathematica общее решение
задачи о колебаниях полубесконечной струны: Постройте с её помощью решение для следующей частной задачи:
Представьте решение графически, как в предыдущем упражнении: в виде двумерного графика для 0 < x < 10, при t = 0.1; 0.5; 1; в виде трёхмерного графика для 0 < x < 10, 0 < t < 1. |