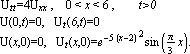Упражнение 12: Введите в Mathematica общее решение
задачи о колебаниях струны с закреплёнными концами: Указание 1: Используйте выражение для решения этой задачи, полученное на практических занятиях. Указание 2: В разложении U(x, t) по гармоникам собственных колебаний 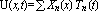 используйте только первые 25 гармоник.Указание 3: Введите сначала конкретные значения функций φ(t) и ψ(t) и параметров a и l (см. примеры ниже), затем вычислите массивы A и B, состоящие из амплитудных коэффициентов A[[n]] и B[[n]] (используйте здесь непосредственное присвоение и команды Table и NIntegrate, т. е. A = Table[NIntegrate[...]...]), а затем определите функцию U(x,t) (т. е. U[x, t] = ..). Постройте решения для следующих частных задач:
Постройте графики решений U(x, t), как функций от x в нтервале 0<x<6 для t = 0.1; 0.5; 1; 1.5; 2. Графики оформите следующим образом:
Ознакомьтесь со значениями других опций команды Plot (выполните команду Options[Plot]). Постройте последовательной графиков U(x, t) для t=0.5i, i=0,1.. 12. Используйте для этого команду Table (т. е. Table[Plot[...]...]). Вы должны получить 13 графиков, представляющих форму струны в моменты времени t=0; 0.5; 1; 1.5; 2; ...; 6. Серните полученную группу графических ячеек, чтоб на экране остался только первый из этих графиков. Теперь выполните их анимацию. Для этого выполните двойной щелчок по первой графической ячейке. На экране должно происходить движение, представляющее собой смену рассчитаных ранее графиков. |
