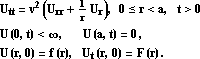
Её решение было построено с помощью метода разделения переменных в виде разложения в ряд по гармоникам собственных колебаний.
Используя это выражение, запишите общее решение задачи с нутевыми начальными скоростями(F(r)=0):
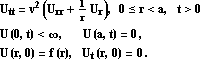
Упражнение 13: Введите полученные формулы в
Mathematica, взяв следующие значения параметров va и функции F(r):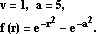 В решении ограничтесь первыми 10 гармониками свободных колебаний. Указание: Используйте функции Mathematica для расчёта функций Бесселя и рассчёта её нулей (BesselJZeros). Обратите внимание, что для использования последней функции необходимо загрузить стандартный пакет Mathematica NumericalMath `BesselJZeros`, для чего требуется выполнить команду <<NumericalMath`BesselJZeros` (см. справку и примеры по BesselJZeros). a) Убедитесь, что введённые выражения позволяют вычислить значение функции U(r, t) для произвольного r в интервале 0≤r<a и произвольного t>0. b) Проверьте, что рассчитанные таким образом значения мало отличаются от точных значений, т. е. от f(r). (Отличие возникает из-за погрешности численных рассчётов и из-за конечности числа гармоник). Постройте график разности U(r, 0) - f(r). c) Увеличте число гармоник, и убедитесь, что отличие U(r, 0) от f(r) уменьшается. Постройте опять график их разности. d) Так же, как это было сделано в предыдущем занятии (для колебаний струны), постройте серию двумерных графиков, на которых изобразите U(r, t) как функцию от r для ряда последовательных моментов времени (например, первый график - U(r, 0.1), второй - U(r, 0.2) и т. д.), а затем выполните их анимацию. e) Просмотрите справку по команде SurfaceOfRevolution и постройте с её помощью трёхмерный график, представляющий круглую мембрану, описываемую функцией U(r, t), в какой-либо фиксированный момент времени t. f) Постройте серию таких трёхмерных графиков для ряда последовательных моментов времени и выполните их анимацию. |
ΔU = 0, 0≤r≤a, 0≤φ≤2π
U(a, φ) = f(φ)
Используйте полученное решение для выполнения следующего задания.
Упражнение 14: Постройте решение данной задачи для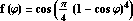 Представьте решение в виде трёхмерного графика на круговой области с помощью команды CylindricalPlot3D. |